১।
করোনা কবলিত এই ধূসর সময়ে আবার ফিরে এলাম বিজ্ঞানের গল্প নিয়ে। বাসায় যখন গন্ডাখানেক নানা বয়সী করোনা রোগী থাকেন, আর দুই শহরের ছুটে চলা জীবনে বাধ্যতামূলক গৃহবন্দীত্ব বরণ করতে হয়, তখন পড়াশোনা করাই ভাল। আর জানেন তো, জ্ঞানবৃক্ষের ফল একলা খেতে নেই, শয়তানিল ব্যাটা যতই উস্কানি দিক না কেন। তাই কাছা মেরে শক্ত হয়ে বসুন, কাছা না থাকলে আগে লুঙ্গি পরে আসুন, কেবল বেনাপোল চলে যাবেন না যেন। গত পর্বে (প্রাগৈতিহাসিক কালের কথা) বলেছিলাম জড় প্রসঙ্গ কাঠামো নামের এক জবড়জং নামের জবরদস্ত জিনিসের কথা। এই জিনিসটি না বুঝলে আপেক্ষিকতার আলাপ-আলোচনা-টকশো করা কঠিন হয়ে যায়, কেন না এর ওপরেই যত হিসেবপাতি। তাই আসুন, এটা আবার বেশ করে বুঝে নিই। তারপর, লোরেনৎস নামে আরেক ভদ্রলোকের সাথে মোলাকাত হবে, অবশ্যই সামাজিক দূরত্ব মেনে।
২।
“প্রসঙ্গ কাঠামো” এই খটরমটর নামটা দিয়ে বিজ্ঞানীরা যা বোঝান, সেটি আসলে আমরা নিয়ত ব্যবহার করছি। এটি আসলে একটি ইচ্ছাধীন খুঁটি, যেটি গেঁড়ে তবেই আমাদের গল্পের গরু (বা ছাগল) বাঁধা চলবে। আমরা যদি একমাত্রা থেকে শুরু করি, তবে বুঝতে সুবিধা হবে। একমাত্রিক কাঠামো হল- যার কেবল দৈর্ঘ্য আছে- তেমন অলম্বুষের মতন লম্বা কিছু, সে যেদিকেই হোক না কেন। ধরুন, কাপড় শুকানোর জন্য ঝোলানো লম্বা একগাছা তার, কিংবা একটা চকের দাগ, কিংবা একটা খুঁটি- এমন। হুমায়ুনের (আজাদ না, আহমেদ) পিপলি বেগমের কথা মনে আছে? মনে করুন, পিপলিকে ধরে এনে একটা ঝোলানো তারের ওপর ছেড়ে দিলাম। তারপর ডিপজলের মতন কণ্ঠে মুহাহাহা করে বললাম- “বালা, নাচো তো দেখি!” এখন পিপলি বেচারা যেহেতু ঝুলে আছে তারের সাথে, সে যেতে পারবে কেবল তার বরাবর- ডাইনে কিংবা বাঁয়ে। এবার পরিস্থিতি আরেকটু জটিল করি? ধরুন, তারের গায়ে প্রতি এক সেন্টিমিটার পরপর কালো দাগ কেটে দিলাম, আর মাঝের দাগে দিলাম লাল রঙ করে। অর্থাৎ, লাল দেখলেই বুঝতে পারব- ঠিক মধ্যিখান কোনটা। একে বইয়ের ভাষায় বলে মূলবিন্দু। আবার, ঐযে কালো-কালো দাগ কাটা হল, সেখান থেকে বুঝতে পারব পিপলি বেগম নাচতে নাচতে কোথায় গেল। চলুন, নিচের ছবিগুলো দেখি-
পিপলি বেগমের নাচ-১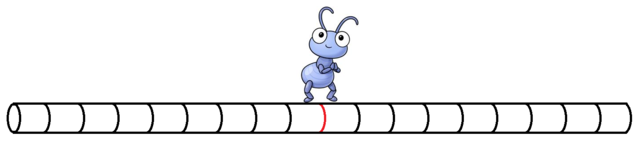
পিপলি বেগমের নাচ-২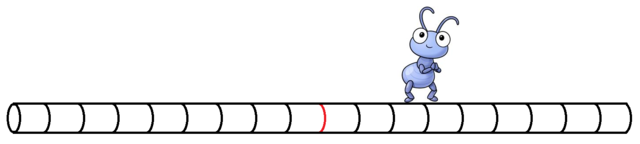
পিপলি বেগমের নাচ-৩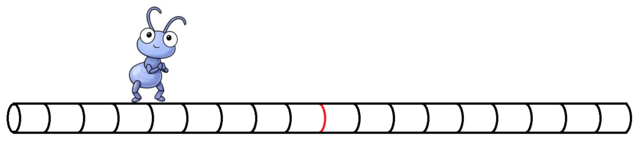
প্রথম ছবিতে পিপলি আছে ঠিক লালদাগে, অর্থাৎ মূলবিন্দুতে। দ্বিতীয় ছবিতে সে আছে ডানদিকের ৩ নং দাগে, আর তৃতীয় ছবিতে বামদিকের ৫ নং দাগে। বইয়ের ভাষায় ডানদিকের কালো দাগগুলিকে নাম দেয়া হয় ১, ২, ৩, ৪… ইত্যাদি আর বামদিকের দাগগুলিকে নাম দেয়া হয় -১, -২, -৩, -৪… ইত্যাদি। বেশি বুদ্ধিমানেরা মনেহয় বুঝে গেছেন- লালদাগের মান আসলে শূন্য। এই সংখ্যা ব্যবহার করে আসলে একটা রেখা বরাবর কোন বিন্দুর অবস্থান চিহ্নিত করা হয়, এক্ষেত্রে মূলবিন্দু থেকে তার দুরত্বই আসলে অবস্থান।
৩।
এবারে আসুন, দ্বিমাত্রিক কাঠামো ব্যাপারটা বুঝে দেখি। দ্বিমাত্রিক কাঠামো আসলে দাবার বোর্ডের মতন চ্যাপ্টা একটা জিনিস। যেমন, একফালি কাগজ, বিছানার টানটান চাদর কিংবা সমান মাঠ- এমন। এখন, মনে করুন পিপলীর তারনৃত্যে মুগ্ধ হয়ে তাকে তারের খাঁচা থেকে মুক্তি দিলাম। কোথায় বলুন তো? একটা দাবার বোর্ডে, যার কোন শেষ নাই। আগের মতই দাবার বোর্ডেও লাল-কালো-সাদা দাগ দিয়ে রাখলাম। তবে এবার তো আর তারের মতন একটা দিক নেই, তাই কেবল ডানে-বাঁয়ে চিন্তা করা যথেষ্ট নয়, একইসাথে ভাবতে হবে সামনে-পেছনেও। দাগটাগ কেটে পিপলি বেগমকে আবার নাচতে লাগিয়ে দিলাম দাবার বোর্ডে। আসুন, ছবিতে তার নাচ দেখি।
পিপলি বেগমের নাচ-৪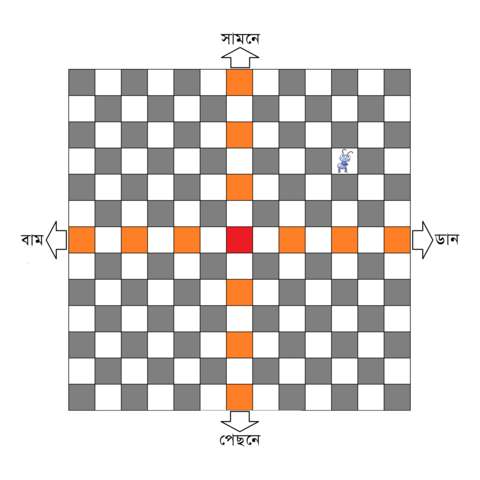
এবারে, ভেনিয়া কাশকিনের মতন “ডাইনে হাল, বাঁয়ে হাল” হুকুম দেয়ার জন্য একটা দাগ, আবার সিঁধেলের মতন “সামনে স্টিয়ারিং, পেছনে স্টিয়ারিং” বলার জন্য আরেকটা দাগ। এই দাগগুলোকে বইয়ের ভাষায় বলে অক্ষ। সাধারণত ডানে-বাঁয়ে আঁকা দাগটাকে নাম দেয়া হয় “এক্স”, আর সামনে-পেছনের জন্য “ওয়াই”। এই দুটি আবার যেখানে একজন আরেকজনের ওপর দিয়ে যায়, সেটাই মূলবিন্দু। মনে রাখবেন, সবার উপরে আছে মধ্যিখান- সেটা ডানও না, বামও না, ওপরেও না, নিচেও না! ঐ যে লালঝান্ডার মতন টকটকে লালরং ঘর, ঐটাই মধ্যিখান- অর্থাৎ মূলবিন্দু। তাহলে, মূলবিন্দুকে খুঁটি ধরে এবার বলা যায় ছবিতে পিপলি আছে ৪ ঘর ডানে এবং ৩ ঘর সামনে। গণিতের ভারিক্কি ভাষায় একে লেখা হয় (৪, ৩) এভাবে। লেখচিত্রের সাথে যাঁরা পরিচিত, তাঁরা বোধহয় চিনতে পারছেন- এদের বলে স্থানাঙ্ক। আর না চিনলেও ক্ষতি নেই- দাবার বোর্ড চিনেছেন তো? ওতেই চলবে।
৪।
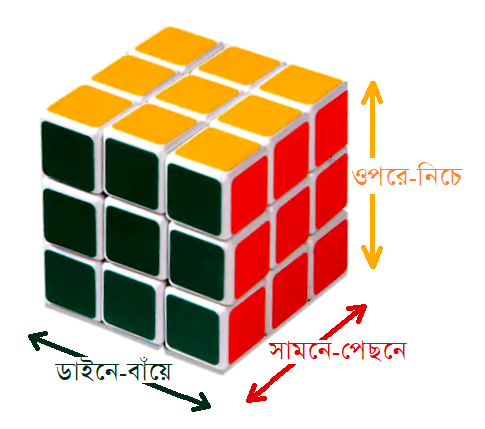
এবার আসুন, মাত্রা আরেকটা বাড়াই। অর্থাৎ, পিপিলীকার পাখা ওঠে মরিবার তরে। ধরুন একমাত্রা আর দুইমাত্রায় নাচ দেখিয়ে পিপলির খুব ডাঁট হয়েছে, একেবারে পাখা গজিয়ে গেছে। তাহলে সে এখন কেবল ডাইনে-বাঁয়ে আর সামনে-পেছনে নয়, বরং ওপরে-নিচে বরাবরও ওঠানামা করতে পারে। যাঁরা বুদ্ধির ঢেঁকি, তাঁরা নিশ্চয় বুঝে গেছেন যে- এবার ঐ তিন নম্বর দিক, অর্থাৎ উর্ধ্ব-অধঃ বোঝাতে আমাদের আরেকটা খুঁটি লাগবে। এবারে, এই ত্রিমাত্রিক ব্যবস্থাটা হবে অনেকটা রুবিক্স কিউবের মতন। রুবিক্স কিউব চেনেন তো? না চিনলে ছবি দেখুন।
রুবিক্স কিউবঃ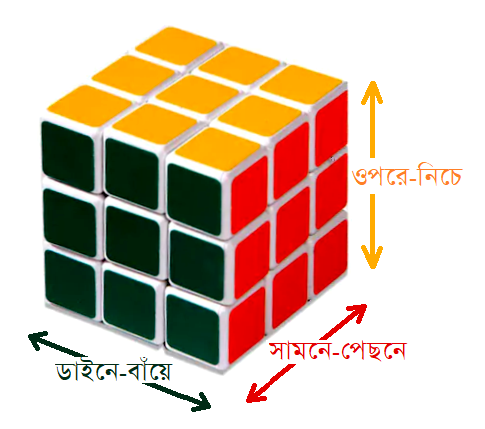
অথবা বহুতল একটা ফ্ল্যাটবাড়ির কথা ভাবুন। যার প্রতি তলায় অনেকগুলো করে ফ্ল্যাট আছে। তাহলে বাড়ি চেনাতে আমাদের কি বলতে হবে? প্রথমে বলতে হবে কত তলায়, তারপর ডাইনে না বাঁয়ে, তারপর আবার সামনে না পেছনে। গনিতের ভাষায়, তিনটি মাত্রায় বা তিনটি অক্ষ বরাবর মোট তিনটি সংখ্যা প্রয়োজন হবে। অর্থাৎ, (২, ৩, ৫) বললে বোঝাবে পাঁচতলায়, সামনের দিকের তিন নম্বর সারির ডানদিকের দ্বিতীয় বাসা। দাবার ছকে যেমন অনেকগুলো বর্গাকার খোপ ছিল, এবারে রুবিক্স কিউবের মতন তিন দিকেই অনেকগুলো ছোট ছোট বাক্সের কথা ভাবুন। ত্রিমাত্রিক কাঠামো ঠিক এমন। এত জটিল করে আঁকা অনেক হ্যাপা, তাই একে সরল করে আঁকা হয় নিচের ছবির মতন করে।
ত্রিমাত্রিক প্রসঙ্গ কাঠামোঃ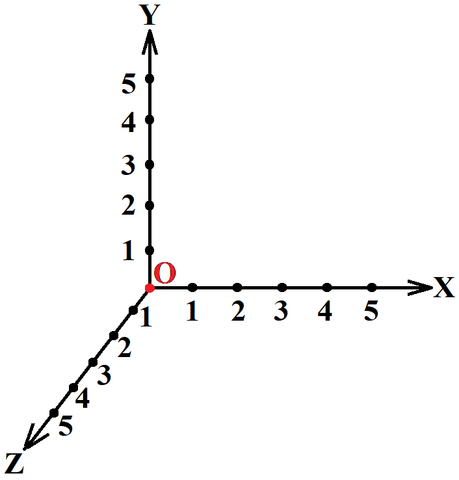
এই হল আমাদের ত্রিমাত্রিক প্রসঙ্গ কাঠামো। গণিতবিদেরা এভাবে একটার পর একটা মাত্রা জুড়তেই থাকেন, আমরা আপাতত তিন মাত্রায় থেমে যাব।
৫।
এমন খটরমটর দেখে ভয় পাবেন না যেন, প্রসঙ্গ কাঠামো বলতেই যে এমন রেখা টেনে, খুঁটি গেড়ে, দাবার ছক বানিয়ে হুলুস্থুল করতে হবে- তা কিন্তু নয়। আমাদের আশেপাশে থাকা চেনাজানা জিনিসও হতে পারে প্রসঙ্গ কাঠামো। ধরুন, মীনা লালী গরুকে খাইয়ে দাইয়ে রাজুর হাতে দিয়ে বলল- “যাও রাজু, ওরে পুকুরপারের থিক্যা মাঠের দিকে যাইতে হাতের ডাইনে তিন নম্বর কাঁঠাল গাছের গোড়ায় বাইন্ধা আসো!” মীনাও কিন্তু আসলে পুকুরকে ‘সাপেক্ষ’ হিসেবে সাক্ষী মেনে একটা প্রসঙ্গ কাঠামোয় বর্ণনা দিল। ধরেন মেলায় বন্দুকবাজি করতে গেলেন বেলুনওয়ালার কাছে। বেলুনওয়ালা সমঝদার খদ্দের পেয়ে বেশ মোলায়েম করে পরামর্শ দিল- “ওপরের সারির তিন নম্বর বেলুনে সই করেন, ভাইজান। লাগবোই লাগবো!” বেলুনওয়ালাও কিন্তু আসলে ব্যবহার করছে একটি প্রসঙ্গ কাঠামো। ধরুন ট্রেনে বেড়াতে যাবেন, আপনার বগি নং-ঞ, কেবিন নং-৬, আর বাংক পেলেন ওপরেরটা। খুঁজে পেতে কি খুব কষ্ট হবে? এই যে নম্বর মিলিয়ে আসন খুঁজে নিচ্ছেন- আপনিও ব্যবহার করছেন একটি প্রসঙ্গ কাঠামো। আমরা যখন বলি অমুক বইটা আছে জানালার পাশের আলমারির, তিন নম্বর তাকে- আমরাও আসলে ঘোষণা করছি একটি ত্রিমাত্রিক প্রসঙ্গ কাঠামো। মিলিটারি স্কুলে থাকতে আমাদের ফৌজি ওস্তাদেরা পান থেকে চুন খসলেই হুকুম দিতেন- “তিন নং ফুটবল মাঠের চারদিকে তিন চক্কর” কিংবা “এই দেয়াল থেকে ঐ দেয়াল, কেয়ামত পর্যন্ত দৌড় হবে!” কি বুঝলেন? আবারো সেই প্রসঙ্গ কাঠামো। ফুটবলের মাঠে কিংবা ক্রিকেটের মাঠে যখন খেলোয়াড়দের অবস্থান নির্দিষ্ট করে দেয়া হয়, সেটিও আসলে প্রসঙ্গ কাঠামোরই ব্যবহার। গোলপোস্ট, কর্ণারফ্ল্যাগ, ডি-বক্সের দাগ আর সেন্টারের দাগদুগ দেখেই আমরা চিনে নেই কোথায় দাঁড়াবে গোলকিপার আর কোথায় স্ট্রাইকার। ক্রিকেটের মাঠেও কিন্তু উইকেট, পিচ আর বাউন্ডারি লাইন দেখেই চট করে বোঝা যায় কোনটা স্লিপ আর কোনটা থার্ড ম্যানের দাঁড়াবার জায়গা। এভাবে প্রতিনিয়ত প্রসঙ্গ কাঠামোর নিগড়ে আমরা বন্দী। আসুন, এবার জড় আর অজড় প্রসঙ্গ কাঠামো বুঝে নিই।
৬।
জড় প্রসঙ্গ কাঠামো হল এমন প্রসঙ্গ কাঠামো, যাদের বেগ একই। বেগ মানে কিন্তু সিরাজের ঘাতক মোহাম্মদী বেগ না! এর অর্থ হল- কত দ্রুত যাচ্ছে সেইটা। প্রতি সেকেন্ডে কোন বস্তু কয় মিটার যাচ্ছে, সাংখ্যিকভাবে এই পরিমাণটাই বেগ। উসাইন বোল্ট ১০০ মিটার দৌড়ুতে সময় নেন প্রায় ১০ সেকেন্ড। অর্থাৎ, প্রতি সেকেন্ডে তিনি যাচ্ছেন ১০ মিটার। এই যে “প্রতিসেকেন্ডে ১০ মিটার” এটাই বোল্টের বেগ। এখন বোল্ট মশায় যদি তাল ঠিক রেখে সারাক্ষণ ঠিক “প্রতি সেকেন্ডে ১০ মিটার” এই হারেই চলেন, তাকে বলে ধ্রুববেগ। বোল্টের কিংবা যে কারো অবস্থান আর বেগ মাপতেও লাগে প্রসঙ্গ কাঠামো। মাঠের মধ্যে লাল-সাদা দাগ দেয়া জায়গায় দৌড়ান বলেই না আমরা তার গতি টের পাই। উনাকে মহাশূন্যে ছেড়ে দিয়ে যদি বলা হয়- “নে বাবা, প্রাণ ভরে দৌড়া!” তখন? এবার কিন্তু আমরাই বিপদে পড়ে যাব, পেছনে কিছু না থাকলে তিনি কত জোরে দৌড়াচ্ছেন মাপা কঠিন বৈকি। এজন্যই কাজে লাগে প্রসঙ্গ কাঠামো। এখন, মনে করুন পাশাপাশি দুটি বাস ছুটছে নির্দিষ্ট মানের বেগে। অর্থাৎ তাদের বেগ বাড়ছে বা কমছে না, একই গতিতে চলছে। এখন তাদের গতি সমান হতে পারে, কম-বেশিও হতে পারে। কিন্তু, কোনও পরিবর্তন যদি না থাকে- তখন এই জোড়াকে বলা হবে “জড় প্রসঙ্গ কাঠামো”। এই কথাটা মনে রাখুন, কেননা বিশেষ আপেক্ষিক তত্ত্বের পুরোটাই জড় প্রসঙ্গ কাঠামোয় ঘটবে। একইভাবে, কোনও কাঠামো জোড়ার যদি বেগের পরিবর্তন হয়- অর্থাৎ বাড়ে-কমে, তখন তারা “অজড় প্রসঙ্গ কাঠামো” হবে। ধরেন, প্ল্যাটফর্ম থেকে একটা ট্রেন ছেড়ে যাচ্ছে। শুরুতে কি হয়? থেমে থাকা ট্রেনের বেগ ধীরে ধীরে বাড়ে, অর্থাৎ বদলায়। এক্ষেত্রে প্ল্যাটফর্ম একটা কাঠামো, আবার ট্রেন আরেকটা কাঠামো। একটি চলন্ত ট্রেন এসে থামলেও একই ব্যপার হবে। যেহেতু এদের একজনের সাপেক্ষে আরেকজনের গতি ‘বদলাচ্ছে’, এরা তাই ‘অজড়’ কাঠামো হবে। আবার ধরুন, যে ট্রেনের স্টপেজ নেই, সেটি তো গতি না কমিয়েই ভোঁসভোঁস করতে করতে ছুটে যাবে একই বেগে- একে আমরা বলব “জড় প্রসঙ্গ কাঠামো”।
আজকের বিজ্ঞানের গল্প এখানেই শেষ।